Deep Learning ושוק ההון

עדכון 15.03.2024 כתבתי את זה לפני יותר משבע שנים. ההבנה שלי התפתחה מאז, ועולם ה־deep learning עבר יותר ממהפכה אחת מאז. זה היה פופולרי בזמנו, ואולי עדיין כיף לקרוא — למרות שסביר שתלמדו מידע מדויק ועדכני יותר במקום אחר

עדכון 25.1.17 — לקח לי זמן אבל הנה מחברת ipython עם מימוש גס

למה NLP רלוונטי לחיזוי מניות

בהרבה בעיות NLP אנחנו בסופו של דבר לוקחים רצף ומקודדים אותו לייצוג יחיד בגודל קבוע, ואז מפענחים את הייצוג הזה לרצף אחר. למשל, אנחנו עשויים לתייג ישויות בטקסט, לתרגם מאנגלית לצרפתית או להמיר תדרי אודיו לטקסט. יש שטף עצום של עבודה שיוצא בתחומים האלה והרבה מהתוצאות מגיעות לביצועים מהטובים ביותר.

בעיניי ההבדל הגדול ביותר בין NLP לניתוח פיננסי הוא שלשפה יש איזושהי הבטחה למבנה, רק שהחוקים של המבנה מעורפלים. שווקים, לעומת זאת, לא מגיעים עם הבטחה למבנה שאפשר ללמוד אותו; ההנחה שמבנה כזה קיים היא מה שהפרויקט הזה אמור היה להוכיח או להפריך (או יותר נכון, אולי להוכיח או להפריך אם אצליח למצוא את המבנה הזה).

בהנחה שהמבנה שם, הרעיון לסכם את מצב השוק הנוכחי באותה צורה שבה אנחנו מקודדים את הסמנטיקה של פסקה נשמע לי סביר. אם זה עדיין לא נשמע הגיוני, המשיכו לקרוא. זה יתחיל להסתדר.

תדע מילה לפי החברה שהיא שומרת (Firth, J. R. 1957:11)

יש המון ספרות על word embeddings. ההרצאה של Richard Socher היא מקום מצוין להתחיל. בקצרה, אפשר ליצור גאומטריה לכל המילים בשפה שלנו, והגאומטריה הזאת לוכדת את המשמעות של מילים ואת היחסים ביניהן. אולי ראיתם את הדוגמה של “King-man +woman=Queen” או משהו בסגנון.

Embeddings מגניבים כי הם מאפשרים לנו לייצג מידע בצורה דחוסה. הדרך הישנה לייצג מילים הייתה להחזיק וקטור (רשימה גדולה של מספרים) שאורכו כמספר המילים שאנחנו מכירים, ולהציב 1 במקום מסוים אם זו המילה הנוכחית שאנחנו מסתכלים עליה. זו לא גישה יעילה, והיא גם לא לוכדת שום משמעות. עם embeddings, אפשר לייצג את כל המילים במספר קבוע של ממדים (300 נראה יותר ממספיק, 50 עובד מצוין) ואז לנצל את הגאומטריה המממדית הגבוהה שלהן כדי להבין אותן.

התמונה למטה מראה דוגמה. embedding אומן פחות או יותר על כל האינטרנט. אחרי כמה ימים של חישובים אינטנסיביים, כל מילה הוטמעה במרחב ממדים גבוה. ל“מרחב” הזה יש גאומטריה, מושגים כמו מרחק, ולכן אפשר לשאול אילו מילים קרובות זו לזו. המחברים/הממציאים של השיטה עשו דוגמה. הנה המילים שהכי קרובות ל־Frog.

אבל אפשר להטמיע יותר מרק מילים. אפשר, למשל, לעשות embeddings לשוק ההון.

Market2Vec

אלגוריתם ה־word embedding הראשון ששמעתי עליו היה word2vec. אני רוצה לקבל אפקט דומה לשוק, למרות שאשתמש באלגוריתם אחר. נתוני הקלט שלי הם csv: העמודה הראשונה היא התאריך, ויש 4*1000 עמודות שמתאימות למחירי High Low Open Closing של 1000 מניות. כלומר וקטור הקלט שלי הוא מממד 4000, שזה גדול מדי. אז הדבר הראשון שאני הולך לעשות הוא לדחוס אותו למרחב ממדים נמוך יותר, נגיד 300 כי אהבתי את הסרט.

לקחת משהו ב־4000 ממדים ולדחוס אותו למרחב של 300 ממדים אולי נשמע קשה, אבל זה בעצם קל. צריך רק להכפיל מטריצות. מטריצה היא גיליון אקסל גדול שיש בו מספרים בכל תא ואין בו בעיות פורמט. תדמיינו טבלה באקסל עם 4000 עמודות ו־300 שורות, וכשאנחנו בעצם דופקים אותה על הווקטור יוצא וקטור חדש שהוא רק בגודל 300. הלוואי שככה היו מסבירים את זה בקולג׳.

התחכום מתחיל כאן: אנחנו נקבע את המספרים במטריצה באקראי, וחלק מה“deep learning” הוא לעדכן את המספרים האלה כך שגיליון האקסל ישתנה. בסופו של דבר למטריצת הגיליון (מעכשיו אקרא לה פשוט מטריצה) יהיו מספרים שמדחסים את הווקטור המקורי בממד 4000 לסיכום תמציתי בממד 300.

אנחנו נהיה קצת יותר מתוחכמים וניישם מה שנקרא פונקציית אקטיבציה. אנחנו ניקח פונקציה וניישם אותה על כל מספר בווקטור בנפרד כך שכולם ייצאו בין 0 ל־1 (או בין 0 לאינסוף — תלוי). למה? זה הופך את הווקטור ליותר “מיוחד”, ומאפשר לתהליך הלמידה שלנו להבין דברים מורכבים יותר. איך?

אז מה? מה שאני מצפה למצוא הוא שההטמעה החדשה של מחירי השוק (הווקטור) למרחב קטן יותר תתפוס את כל המידע החיוני למשימה, בלי לבזבז זמן על דברים אחרים. אז הייתי מצפה שהיא תלכוד קורלציות בין מניות אחרות, אולי תזהה מתי סקטור מסוים נחלש או מתי השוק מאוד “חם”. אני לא יודע אילו תכונות היא תמצא, אבל אני מניח שהן יהיו שימושיות.

אז מה עכשיו

בואו נשים רגע בצד את וקטורי השוק שלנו ונדבר על מודלי שפה. Andrej Karpathy כתב את הפוסט האפי “The Unreasonable effectiveness of Recurrent Neural Networks”. אם אסכם בצורה הכי ליברלית, הפוסט מצטמצם ל:

1. אם נסתכל על הכתבים של שייקספיר ונעבור עליהם תו־תו, אפשר להשתמש ב“deep learning” כדי ללמוד מודל שפה.
2. מודל שפה (במקרה הזה) הוא קופסה קסומה. נותנים לו את כמה התווים הראשונים והוא אומר מה יהיה התו הבא.
3. אם ניקח את התו שמודל השפה חזה ונאכיל אותו חזרה פנימה, נוכל להמשיך לנצח.

ואז כפואנטה, הוא יצר המון טקסט שנראה כמו שייקספיר. ואז הוא עשה את זה שוב עם קוד המקור של לינוקס. ואז שוב עם ספר לימוד על גאומטריה אלגברית.

אז עוד רגע אחזור למכניקה של הקופסה הקסומה הזו, אבל אזכיר שאנחנו רוצים לחזות את השוק העתידי על בסיס העבר בדיוק כמו שהוא חזה את המילה הבאה על בסיס הקודמת. איפה ש־Karpathy השתמש בתווים, אנחנו נשתמש בוקטורי השוק שלנו ונאכיל אותם לקופסה השחורה הקסומה. עדיין לא החלטנו מה אנחנו רוצים שהיא תחזה, אבל זה בסדר — גם לא נאכיל את הפלט שלה חזרה פנימה.

להעמיק

אני רוצה להדגיש שזה המקום שבו אנחנו מתחילים להיכנס ל־deep של deep learning. עד עכשיו יש לנו רק שכבת למידה אחת — גיליון האקסל שמדחס את השוק. עכשיו נוסיף עוד כמה שכבות ונערום אותן כדי לעשות משהו “עמוק”. זה ה־deep ב־deep learning.

אז Karpathy מראה לנו פלט לדוגמה מקוד המקור של לינוקס — זה משהו שהקופסה השחורה שלו כתבה.

static void action_new_function(struct s_stat_info *wb)
{
  unsigned long flags;
  int lel_idx_bit = e->edd, *sys & ~((unsigned long) *FIRST_COMPAT);
  buf[0] = 0xFFFFFFFF & (bit << 4);
  min(inc, slist->bytes);
  printk(KERN_WARNING "Memory allocated %02x/%02x, "
    "original MLL instead\n"),
    min(min(multi_run - s->len, max) * num_data_in),
    frame_pos, sz + first_seg);
  div_u64_w(val, inb_p);
  spin_unlock(&disk->queue_lock);
  mutex_unlock(&s->sock->mutex);
  mutex_unlock(&func->mutex);
  return disassemble(info->pending_bh);
}

שימו לב שהוא יודע לפתוח ולסגור סוגריים, ומכבד מוסכמות הזחה; תוכן הפונקציה מוזח נכון והמשפט הרב־שורי printk מכיל הזחה פנימית. זה אומר שהקופסה הקסומה הזו מבינה תלות לטווח ארוך. כשהיא מזיחה בתוך משפט print היא יודעת שהיא בתוך משפט print וגם זוכרת שהיא בתוך פונקציה (או לפחות בתוך scope מוזח אחר). זה מטורף. קל לדלג מעל זה, אבל אלגוריתם שיש לו יכולת ללכוד ולזכור תלות ארוכת טווח הוא מאוד שימושי כי… אנחנו רוצים למצוא תלות ארוכת טווח בשוק.

בתוך הקופסה השחורה הקסומה

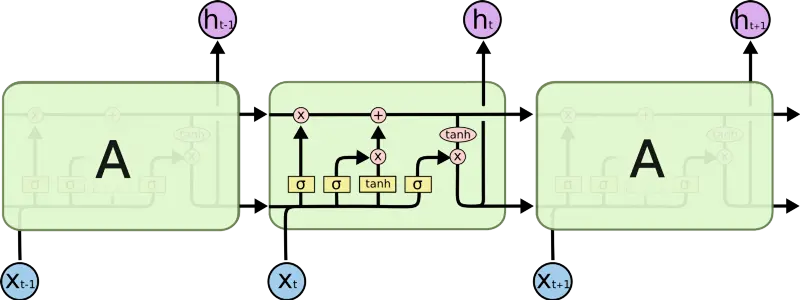
מה יש בתוך הקופסה השחורה הקסומה הזו? זה סוג של Recurrent Neural Network (RNN) שנקרא LSTM. RNN הוא אלגוריתם deep learning שפועל על רצפים (כמו רצפים של תווים). בכל צעד, הוא לוקח ייצוג של התו הבא (כמו ה־embeddings שדיברנו עליהם קודם) ומפעיל על הייצוג מטריצה, כמו שראינו קודם. העניין הוא של־RNN יש סוג של זיכרון פנימי, כך שהוא זוכר מה הוא ראה בעבר. הוא משתמש בזיכרון הזה כדי להחליט איך בדיוק לפעול על הקלט הבא. בעזרת הזיכרון הזה, ה־RNN יכול “לזכור” שהוא בתוך scope מוזח — וככה אנחנו מקבלים טקסט פלט מקונן נכון.

גרסה “מפונפנת” של RNN נקראת Long Short Term Memory (LSTM). ל־LSTM יש זיכרון שתוכנן בחוכמה כך שהוא מאפשר לו:

1. לבחור באופן סלקטיבי מה לזכור
2. להחליט לשכוח
3. לבחור כמה מהזיכרון שלו להוציא כפלט.

אז LSTM יכול לראות “{“ ולהגיד לעצמו “אה כן, זה חשוב — אני צריך לזכור את זה”, וכשהוא עושה זאת הוא בעצם שומר אינדיקציה לכך שהוא בתוך scope מקונן. אחרי שהוא רואה את ה־“}” המתאים, הוא יכול להחליט לשכוח את הסוגר המסולסל הפותח המקורי ובכך לשכוח שהוא בתוך scope מקונן.

אנחנו יכולים לגרום ל־LSTM ללמוד מושגים מופשטים יותר על ידי ערימה של כמה LSTM אחד מעל השני, וזה יחזיר אותנו להיות “Deep” שוב. עכשיו כל פלט של ה־LSTM הקודם הופך לקלט של הבא, וכל אחד ממשיך ללמוד הפשטות גבוהות יותר של הנתונים הנכנסים. בדוגמה למעלה (וזו רק ספקולציה להמחשה), שכבת ה־LSTM הראשונה אולי תלמד שתווים שמופרדים ברווח הם “מילים”. השכבה הבאה אולי תלמד טיפוסי מילים כמו (**static** **void** **action_new_function).**השכבה הבאה אולי תלמד את המושג של פונקציה והארגומנטים שלה וכן הלאה. קשה לדעת בדיוק מה כל שכבה עושה, למרות שלבלוג של Karpathy יש דוגמה ממש יפה איך הוא המחיש את זה.

חיבור בין Market2Vec ל־LSTMs

הקורא החרוץ ישים לב ש־Karpathy השתמש בתווים כקלטים שלו, לא ב־embeddings (טכנית, one-hot encoding של תווים). אבל Lars Eidnes למעשה השתמש ב־word embeddings כשכתב Auto-Generating Clickbait With Recurrent Neural Network

האיור למעלה מראה את הרשת שהוא השתמש בה. התעלמו מחלק ה־SoftMax (נגיע לזה אחר כך). לעת עתה, שימו לב איך בתחתית הוא מכניס רצף של word vectors וכל אחד מהם. (זכרו: “word vector” הוא ייצוג של מילה בצורת אוסף מספרים, כמו שראינו בתחילת הפוסט). Lars מכניס רצף של Word Vectors וכל אחד מהם:

1. משפיע על ה־LSTM הראשון
2. גורם ל־LSTM שלו להוציא משהו ל־LSTM שמעליו
3. גורם ל־LSTM שלו להוציא משהו ל־LSTM של המילה הבאה

אנחנו נעשה אותו דבר עם הבדל אחד: במקום word vectors נכניס “MarketVectors”, אותם וקטורי שוק שתיארנו קודם. כדי לסכם, ה־MarketVectors אמורים להכיל סיכום של מה שקורה בשוק בנקודת זמן נתונה. על ידי העברת רצף שלהם דרך LSTMs אני מקווה ללכוד את הדינמיקה ארוכת הטווח שהתרחשה בשוק. על ידי ערימה של כמה שכבות LSTM אני מקווה ללכוד הפשטות ברמה גבוהה יותר של התנהגות השוק.

מה יוצא החוצה

עד כה לא דיברנו בכלל על איך האלגוריתם באמת לומד משהו; רק דיברנו על כל הטרנספורמציות החכמות שנעשה על הנתונים. נדחה את השיחה הזאת לכמה פסקאות למטה, אבל בבקשה זכרו את החלק הזה כי הוא ההכנה לפאנץ׳־ליין שהופך את כל השאר לכדאי.

בדוגמה של Karpathy, הפלט של ה־LSTMs הוא וקטור שמייצג את התו הבא באיזשהו ייצוג מופשט. בדוגמה של Eidnes, הפלט של ה־LSTMs הוא וקטור שמייצג מה תהיה המילה הבאה במרחב מופשט. השלב הבא בשני המקרים הוא להפוך את הייצוג המופשט הזה לווקטור הסתברויות — רשימה שאומרת עד כמה סביר שכל תו או מילה בהתאמה יופיעו הבאים. זו העבודה של פונקציית SoftMax. ברגע שיש לנו רשימת הסתברויות אנחנו בוחרים את התו או המילה שהכי סביר שיופיעו הבאים.

במקרה שלנו, של “חיזוי השוק”, אנחנו צריכים לשאול את עצמנו מה בדיוק אנחנו רוצים שהשוק יחזה? כמה אפשרויות שחשבתי עליהן היו:

1. לחזות את המחיר הבא לכל אחת מ־1000 המניות
2. לחזות את הערך של איזה אינדקס (S&P, VIX וכו׳) בעוד n דקות.
3. לחזות אילו מניות יעלו ביותר מ־x% בעוד n דקות
4. (האהוב עליי אישית) לחזות אילו מניות יעלו/ירדו ב־2x% בעוד n דקות, תוך שהן לא יורדות down/up ביותר מ־x% בזמן הזה.
5. (זה שנמשיך איתו לאורך שאר המאמר). לחזות מתי ה־VIX יעלה/ירד ב־2x% בעוד n דקות, תוך שהוא לא יורד down/up ביותר מ־x% בזמן הזה.

1 ו־2 הן בעיות רגרסיה, שבהן צריך לחזות מספר ממשי ולא הסתברות לאירוע ספציפי (כמו הופעת האות n או עליית השוק). זה בסדר, אבל לא מה שאני רוצה לעשות.

3 ו־4 די דומות; שתיהן מבקשות לחזות אירוע (בז׳רגון טכני — תווית מחלקה). אירוע יכול להיות הופעת האות n הבאה או עלה 5% תוך שלא ירד יותר מ־3% בעשר הדקות האחרונות. ההחלפה בין 3 ל־4 היא ש־3 הרבה יותר נפוץ ולכן קל יותר ללמוד עליו, בעוד 4 יותר בעל ערך כי הוא לא רק אינדיקטור לרווח אלא גם כולל אילוץ על סיכון.

5 הוא זה שנמשיך איתו במאמר הזה כי הוא דומה ל־3 ול־4 אבל עם מכניקה שקל יותר לעקוב אחריה. ה־VIX נקרא לפעמים מדד הפחד והוא מייצג עד כמה המניות ב־S&P500 תנודתיות. הוא נגזר מהתבוננות ב־implied volatility עבור אופציות ספציפיות על כל אחת מהמניות במדד.

הערת אגב — למה לחזות את ה־VIX

מה שהופך את ה־VIX ליעד מעניין הוא ש:

1. זה מספר אחד בלבד, בניגוד לאלפים של מניות. זה מקל על המעקב ברמה המושגית ומפחית עלויות חישוב.
2. זה סיכום של הרבה מניות, אז רוב אם לא כל הקלטים שלנו רלוונטיים.
3. זו לא קומבינציה ליניארית של הקלטים שלנו. implied volatility מופק מנוסחה מסובכת ולא־ליניארית מניה־מניה. ה־VIX נגזר מעל זה מנוסחה מורכבת נוספת. אם נוכל לחזות את זה — זה די מגניב.
4. אפשר לסחור בו, אז אם זה באמת עובד נוכל להשתמש בזה.

חזרה לפלטים של ה־LSTM ול־SoftMax

איך משתמשים בניסוחים שראינו קודם כדי לחזות שינויים ב־VIX כמה דקות קדימה? עבור כל נקודה בדאטה־סט שלנו, נבדוק מה קרה ל־VIX 5 דקות אחר כך. אם הוא עלה ביותר מ־1% בלי לרדת ביותר מ־0.5% במהלך הזמן הזה נוציא 1, אחרת 0. ואז נקבל רצף שנראה כך:

0,0,0,0,0,1,1,0,0,0,1,1,0,0,0,0,1,1,1,0,0,0,0,0 ….

אנחנו רוצים לקחת את הווקטור שה־LSTMs מוציאים ולדחוס אותו כך שייתן לנו את ההסתברות שהפריט הבא ברצף שלנו יהיה 1. הדחיסה מתרחשת בחלק ה־SoftMax בתרשים למעלה. (טכנית, מכיוון שיש לנו עכשיו רק מחלקה אחת, אנחנו משתמשים ב־sigmoid).

אז לפני שניכנס לאיך הדבר הזה לומד, בואו נסכם מה עשינו עד עכשיו:

1. אנחנו מקבלים כקלט רצף של נתוני מחיר עבור 1000 מניות
2. כל נקודת זמן ברצף היא צילום־מצב של השוק. הקלט שלנו הוא רשימה של 4000 מספרים. אנחנו משתמשים בשכבת embedding כדי לייצג את המידע המרכזי ב־300 מספרים בלבד.
3. עכשיו יש לנו רצף של embeddings של השוק. אנחנו מכניסים אותם לערימה של LSTMs, צעד־זמן אחרי צעד־זמן. ה־LSTMs זוכרים דברים מהצעדים הקודמים וזה משפיע על איך הם מעבדים את הנוכחי.
4. אנחנו מעבירים את הפלט של השכבה הראשונה של ה־LSTMs לשכבה נוספת. החבר׳ה האלה גם זוכרים, והם לומדים הפשטות ברמה גבוהה יותר של המידע שהכנסנו.
5. לבסוף, אנחנו לוקחים את הפלט מכל ה־LSTMs ו“דוחסים” אותו כך שרצף מידע השוק יהפוך לרצף הסתברויות. ההסתברות המדוברת היא: “מה הסיכוי שה־VIX יעלה 1% בחמש הדקות הבאות בלי לרדת 0.5%?”

איך הדבר הזה לומד?

עכשיו החלק הכיפי. כל מה שעשינו עד עכשיו נקרא forward pass; היינו עושים את כל הצעדים האלה גם בזמן אימון האלגוריתם וגם כשמשתמשים בו בפרודקשן. כאן נדבר על ה־backward pass — החלק שעושים רק בזמן האימון, והוא זה שגורם לאלגוריתם ללמוד.

אז בזמן אימון, לא רק שהכנו שנים של נתונים היסטוריים, אלא גם הכנו רצף של יעדי חיזוי — אותה רשימת 0 ו־1 שמראה אם ה־VIX זז בצורה שרצינו או לא אחרי כל תצפית בנתונים שלנו.

כדי ללמוד, נאכיל את נתוני השוק לרשת ונשווה את הפלט שלה למה שחישבנו. ההשוואה אצלנו תהיה פשוט חיסור — כלומר נגיד שהשגיאה של המודל שלנו היא:

ERROR = (((precomputed)— (predicted probability))² )^(1/2)

או באנגלית, השורש הריבועי של ריבוע ההפרש בין מה שקרה בפועל לבין מה שחזינו.

הנה היופי: זו פונקציה דיפרנציאלית, כלומר אפשר לומר בכמה השגיאה הייתה משתנה אם התחזית שלנו הייתה משתנה קצת. התחזית שלנו היא התוצאה של פונקציה דיפרנציאלית — ה־SoftMax. הקלטים ל־softmax, ה־LSTMs, כולם פונקציות מתמטיות שניתנות לגזירה. עכשיו כל הפונקציות האלה מלאות בפרמטרים — גיליונות האקסל הגדולים שדיברתי עליהם לפני עידן ועידנים. אז בשלב הזה אנחנו לוקחים את הנגזרת של השגיאה ביחס לכל אחד ממיליוני הפרמטרים בכל גיליונות האקסל האלה במודל. כשעושים את זה רואים איך השגיאה תשתנה כשנשנה כל פרמטר, ולכן נשנה כל פרמטר בצורה שתקטין את השגיאה.

התהליך הזה מתפשט עד להתחלה של המודל. הוא משנה את הדרך שבה אנחנו מטמיעים את הקלטים ל־MarketVectors כך שה־MarketVectors ייצגו את המידע המשמעותי ביותר למשימה שלנו.

הוא משנה מתי ומה כל LSTM בוחר לזכור כך שהפלטים שלהם יהיו הרלוונטיים ביותר למשימה.

הוא משנה את ההפשטות שה־LSTMs לומדים כך שהם ילמדו את ההפשטות החשובות ביותר למשימה.

וזה בעיניי מדהים כי יש לנו פה כל כך הרבה מורכבות והפשטה שמעולם לא היינו צריכים לפרט בשום מקום. הכול מוסק “MathaMagically” מההגדרה של מה אנחנו מחשיבים לשגיאה.

מה הלאה

עכשיו, אחרי שכתבתי את זה וזה עדיין נשמע לי הגיוני, אני רוצה:

1. לראות אם מישהו בכלל טורח לקרוא את זה.
2. לתקן את כל הטעויות שהקוראים היקרים שלי מצביעים עליהן
3. לשקול אם זה עדיין אפשרי
4. ולבנות את זה

אז אם הגעתם עד כאן, בבקשה הצביעו על השגיאות שלי ושתפו את התובנות שלכם.

מחשבות נוספות

הנה כמה מחשבות (בעיקר מתקדמות יותר) על הפרויקט הזה — מה עוד אולי אנסה ולמה זה נשמע לי הגיוני שזה באמת עשוי לעבוד.

נזילות ושימוש יעיל בהון

באופן כללי, ככל ששוק מסוים יותר נזיל, כך הוא יעיל יותר. אני חושב שזה נובע ממעגל של ביצה ותרנגולת: ככל ששוק נהיה נזיל יותר, הוא מסוגל לספוג יותר הון שנכנס ויוצא בלי שההון הזה “יפגע בעצמו”. ככל ששוק נהיה נזיל יותר וניתן להשתמש בו ביותר הון, תמצאו יותר שחקנים מתוחכמים שנכנסים. זה כי להיות מתוחכם זה יקר, ולכן צריך להפיק תשואות על נתח גדול של הון כדי להצדיק את עלויות התפעול.

מסקנה משנית מהירה היא שבשווקים פחות נזילים התחרות לא ממש מתוחכמת באותה מידה, ולכן ההזדמנויות שמערכת כזו יכולה להביא אולי עדיין לא נסגרו. כלומר, אם הייתי מנסה לסחור בזה, הייתי מנסה לסחור במקטעים פחות נזילים של השוק — אולי TASE 100 במקום S&P 500.

הדבר הזה חדש

הידע על האלגוריתמים האלה, המסגרות להריץ אותם וכוח החישוב כדי לאמן אותם — כולם חדשים, לפחות במובן שהם זמינים לג׳ו הממוצע כמוני. אני מניח ששחקנים גדולים פתרו את זה לפני שנים ויכלו להריץ את זה כבר זמן רב, אבל כפי שציינתי בפסקה למעלה, הם כנראה פועלים בשווקים נזילים שיכולים לתמוך בגודל שלהם. הדרג הבא של משתתפי השוק, אני מניח, בעל קצב איטי יותר של אימוץ טכנולוגי, ובמובן הזה יש או בקרוב תהיה תחרות ליישם את זה בשווקים שעדיין לא נוגעים בהם.

מסגרות זמן מרובות

למרות שציינתי זרם יחיד של קלטים למעלה, אני מדמיין שדרך יעילה יותר לאמן תהיה לאמן וקטורי שוק (לפחות) על פני מסגרות זמן מרובות ולהזין אותם בשלב ה־inference. כלומר, מסגרת הזמן הנמוכה ביותר שלי תהיה דגימה כל 30 שניות, והייתי מצפה שהרשת תלמד תלות שמגיעה לכל היותר למתיחות של שעות.

אני לא יודע אם זה רלוונטי או לא, אבל אני חושב שיש תבניות במסגרות זמן מרובות, ואם אפשר להוריד את עלות החישוב מספיק אז כדאי לשלב אותן במודל. אני עדיין מתחבט איך הכי טוב לייצג את זה על הגרף החישובי, ואולי זה לא חובה כדי להתחיל.

MarketVectors

כשמשתמשים ב־word vectors ב־NLP לרוב מתחילים עם מודל מאומן מראש וממשיכים לכוונן את ה־embeddings במהלך אימון המודל שלנו. במקרה שלי אין market vector מאומן מראש זמין, וגם אין אלגוריתם ברור לאימון שלהם.

השיקול המקורי שלי היה להשתמש ב־auto-encoder כמו ב־המאמר הזה, אבל אימון מקצה לקצה יותר מגניב.

שיקול רציני יותר הוא ההצלחה של מודלי sequence to sequence בתרגום ובהכרה בדיבור, שבהם רצף מקודד בסופו של דבר לווקטור יחיד ואז מפוענח לייצוג אחר (כמו מדיבור לטקסט או מאנגלית לצרפתית). במבט הזה, כל הארכיטקטורה שתיארתי היא בעצם ה־encoder, ולא ממש פירטתי decoder.

אבל אני רוצה להשיג משהו ספציפי עם השכבה הראשונה — זו שלוקחת כקלט את הווקטור בממד 4000 ומוציאה וקטור בממד 300. אני רוצה שהיא תמצא קורלציות או יחסים בין מניות שונות ותיצור מאפיינים מהן.

האלטרנטיבה היא להעביר כל קלט דרך LSTM, אולי לשרשר (concatenate) את כל וקטורי הפלט ולהחשיב את זה כפלט של שלב ה־encoder. אני חושב שזה יהיה לא יעיל כי האינטראקציות והקורלציות בין מכשירים לבין המאפיינים שלהם יאבדו, ויידרש פי־10 יותר חישוב. מצד שני, ארכיטקטורה כזו יכולה במובן נאיבי להיות מקבילית על פני כמה GPUs ומכונות, שזה יתרון.

CNNs

לאחרונה היה גל של מאמרים על תרגום מכונה ברמת התו. המאמר הזה תפס לי את העין, כי הם מצליחים ללכוד תלות ארוכת טווח בעזרת שכבה קונבולוציונית במקום RNN. לא קראתי אותו יותר מקריאה מהירה, אבל אני חושב ששינוי שבו אתייחס לכל מניה כערוץ ואבצע קונבולוציה על פני ערוצים תחילה (כמו בתמונות RGB) יכול להיות דרך נוספת ללכוד את דינמיקת השוק — באותה צורה שבה הם בעצם מקודדים משמעות סמנטית מתווים.