Deep Learning The Stock Market

Update 15.03.2024 Ich habe das vor mehr als sieben Jahren geschrieben. Mein Verständnis hat sich seitdem weiterentwickelt, und die Welt des Deep Learning hat seitdem mehr als eine Revolution durchlaufen. Damals war es populär und ist vielleicht immer noch eine unterhaltsame Lektüre, auch wenn du anderswo wahrscheinlich genauere und aktuellere Informationen findest

Update 25.1.17 — Hat eine Weile gedauert, aber hier ist ein ipython notebook mit einer groben Implementierung

Warum NLP für Aktienprognosen relevant ist

In vielen NLP-Problemen nehmen wir am Ende eine Sequenz und kodieren sie in eine einzelne, fest große Repräsentation, und dekodieren diese Repräsentation dann in eine andere Sequenz. Zum Beispiel könnten wir Entitäten im Text markieren, von Englisch nach Französisch übersetzen oder Audiofrequenzen in Text umwandeln. In diesen Bereichen kommt eine Flut an Arbeiten heraus, und viele Ergebnisse erreichen State-of-the-Art-Performance.

Meiner Ansicht nach ist der größte Unterschied zwischen NLP und Finanzanalyse, dass Sprache eine gewisse Garantie für Struktur hat – nur sind die Regeln dieser Struktur vage. Märkte hingegen kommen nicht mit dem Versprechen einer lernbaren Struktur; dass eine solche Struktur existiert, ist die Annahme, die dieses Projekt beweisen oder widerlegen würde (bzw. beweisen oder widerlegen könnte, wenn ich diese Struktur finde).

Wenn wir annehmen, dass die Struktur da ist, erscheint mir die Idee plausibel, den aktuellen Zustand des Marktes so zusammenzufassen, wie wir die Semantik eines Absatzes kodieren. Wenn das noch keinen Sinn ergibt, lies weiter. Es wird.

Man soll ein Wort an der Gesellschaft erkennen, die es hält (Firth, J. R. 1957:11)

Es gibt jede Menge Literatur zu Word Embeddings. Richard Sochers Vortrag ist ein großartiger Einstieg. Kurz gesagt: Wir können eine Geometrie aller Wörter in unserer Sprache konstruieren, und diese Geometrie erfasst die Bedeutung von Wörtern und die Beziehungen zwischen ihnen. Du hast vielleicht das Beispiel „King-man +woman=Queen“ oder so ähnlich gesehen.

Embeddings sind cool, weil sie uns erlauben, Informationen in komprimierter Form darzustellen. Die alte Art, Wörter zu repräsentieren, war, einen Vektor (eine große Liste von Zahlen) zu halten, der so lang ist wie die Anzahl der Wörter, die wir kennen, und eine 1 an eine bestimmte Stelle zu setzen, wenn das das aktuelle Wort ist, das wir betrachten. Das ist weder effizient noch trägt es irgendeine Bedeutung. Mit Embeddings können wir alle Wörter in einer festen Anzahl an Dimensionen darstellen (300 scheinen völlig zu reichen, 50 funktionieren großartig) und dann ihre höherdimensionale Geometrie nutzen, um sie zu verstehen.

Das Bild unten zeigt ein Beispiel. Ein Embedding wurde auf mehr oder weniger dem gesamten Internet trainiert. Nach ein paar Tagen intensiver Berechnungen wurde jedes Wort in einem hochdimensionalen Raum eingebettet. Dieser „Raum“ hat eine Geometrie, Konzepte wie Distanz, und so können wir fragen, welche Wörter nah beieinander liegen. Die Autoren/Erfinder dieser Methode haben ein Beispiel gemacht. Hier sind die Wörter, die am nächsten bei Frog liegen.

Aber wir können mehr als nur Wörter einbetten. Wir können zum Beispiel Stock-Market-Embeddings machen.

Market2Vec

Der erste Word-Embedding-Algorithmus, von dem ich gehört habe, war word2vec. Ich will denselben Effekt für den Markt erzielen, auch wenn ich einen anderen Algorithmus verwenden werde. Meine Eingangsdaten sind ein csv: Die erste Spalte ist das Datum, und es gibt 4*1000 Spalten, die den High-, Low-, Open- und Closing-Preis von 1000 Aktien entsprechen. Das heißt, mein Input-Vektor ist 4000-dimensional, was zu groß ist. Also werde ich als Erstes ihn in einen niedrigdimensionalen Raum stopfen, sagen wir 300, weil mir der Film gefallen hat.

Etwas in 4000 Dimensionen zu nehmen und in einen 300-dimensionalen Raum zu stopfen klingt vielleicht schwierig, ist aber eigentlich einfach. Wir müssen nur Matrizen multiplizieren. Eine Matrix ist eine große Excel-Tabelle, die in jeder Zelle Zahlen hat und keine Formatierungsprobleme. Stell dir eine Excel-Tabelle mit 4000 Spalten und 300 Zeilen vor, und wenn wir sie im Grunde gegen den Vektor „knallen“, kommt ein neuer Vektor heraus, der nur noch Größe 300 hat. So hätte man es mir im Studium erklären sollen.

Die „Fanciness“ beginnt hier: Wir werden die Zahlen in unserer Matrix zufällig initialisieren, und ein Teil des „Deep Learning“ besteht darin, diese Zahlen zu aktualisieren, sodass sich unsere Excel-Tabelle verändert. Schließlich wird diese Matrix (ich bleibe ab jetzt bei Matrix) Zahlen enthalten, die unseren ursprünglichen 4000-dimensionalen Vektor in eine prägnante 300-dimensionale Zusammenfassung von sich selbst überführen.

Wir werden hier noch ein bisschen schicker und wenden das an, was man eine Aktivierungsfunktion nennt. Wir nehmen eine Funktion und wenden sie auf jede Zahl im Vektor einzeln an, sodass am Ende alles zwischen 0 und 1 liegt (oder zwischen 0 und unendlich, je nachdem). Warum? Es macht unseren Vektor „besonderer“ und macht unseren Lernprozess in der Lage, kompliziertere Dinge zu verstehen. Wie?

Na und? Was ich erwarte, ist, dass das neue Embedding der Marktpreise (der Vektor) in einen kleineren Raum alle wesentlichen Informationen für die jeweilige Aufgabe erfasst, ohne Zeit mit dem anderen Kram zu verschwenden. Ich würde also erwarten, dass es Korrelationen zwischen Aktien erfasst, vielleicht erkennt, wenn ein bestimmter Sektor fällt oder wenn der Markt sehr heiß läuft. Ich weiß nicht, welche Merkmale es finden wird, aber ich nehme an, dass sie nützlich sein werden.

Und jetzt?

Lass uns unsere Marktvektoren für einen Moment beiseitelegen und über Sprachmodelle sprechen. Andrej Karpathy schrieb den epischen Beitrag „The Unreasonable effectiveness of Recurrent Neural Networks“. Wenn ich den Beitrag sehr großzügig zusammenfassen würde, läuft er auf Folgendes hinaus:

1. Wenn wir uns die Werke Shakespeares anschauen und sie Zeichen für Zeichen durchgehen, können wir mit „Deep Learning“ ein Sprachmodell lernen.
2. Ein Sprachmodell (in diesem Fall) ist eine magische Box. Du gibst die ersten paar Zeichen hinein, und es sagt dir, was als Nächstes kommt.
3. Wenn wir das Zeichen, das das Sprachmodell vorhergesagt hat, nehmen und wieder hineinfüttern, können wir ewig weitermachen.

Und dann, als Pointe, generierte er einen Haufen Text, der wie Shakespeare aussieht. Und dann tat er es noch einmal mit dem Linux-Quellcode. Und dann wieder mit einem Lehrbuch über algebraische Geometrie.

Ich komme gleich wieder zur Mechanik dieser magischen Box zurück, aber lass mich dich daran erinnern, dass wir die zukünftige Marktentwicklung auf Basis der Vergangenheit vorhersagen wollen – genau so, wie er das nächste Wort auf Basis des vorherigen vorhergesagt hat. Wo Karpathy Zeichen benutzt hat, werden wir unsere Marktvektoren verwenden und sie in die magische schwarze Box füttern. Wir haben noch nicht entschieden, was sie vorhersagen soll, aber das ist okay; wir werden ihre Ausgabe auch nicht wieder zurück in sie einspeisen.

Tiefer gehen

Ich möchte darauf hinweisen, dass wir hier in den „deep“-Teil von Deep Learning einsteigen. Bisher haben wir nur eine einzelne Schicht Lernen: diese Excel-Tabelle, die den Markt kondensiert. Jetzt werden wir ein paar weitere Schichten hinzufügen und sie stapeln, um etwas „Tiefes“ zu bauen. Das ist das „deep“ in Deep Learning.

Karpathy zeigt uns einige Beispielausgaben aus dem Linux-Quellcode – das ist Zeug, das seine schwarze Box geschrieben hat.

static void action_new_function(struct s_stat_info *wb)
{
  unsigned long flags;
  int lel_idx_bit = e->edd, *sys & ~((unsigned long) *FIRST_COMPAT);
  buf[0] = 0xFFFFFFFF & (bit << 4);
  min(inc, slist->bytes);
  printk(KERN_WARNING "Memory allocated %02x/%02x, "
    "original MLL instead\n"),
    min(min(multi_run - s->len, max) * num_data_in),
    frame_pos, sz + first_seg);
  div_u64_w(val, inb_p);
  spin_unlock(&disk->queue_lock);
  mutex_unlock(&s->sock->mutex);
  mutex_unlock(&func->mutex);
  return disassemble(info->pending_bh);
}

Beachte, dass es weiß, wie man Klammern öffnet und schließt und Einrückungskonventionen respektiert; der Inhalt der Funktion ist korrekt eingerückt und die mehrzeilige printk-Anweisung hat eine innere Einrückung. Das bedeutet, dass diese magische Box Langstreckenabhängigkeiten versteht. Wenn sie innerhalb der print-Anweisung einrückt, weiß sie, dass sie in einer print-Anweisung ist, und erinnert sich außerdem daran, dass sie in einer Funktion ist (oder zumindest in einem anderen eingerückten Scope). Das ist verrückt. Man übersieht das leicht, aber ein Algorithmus, der langfristige Abhängigkeiten erfassen und behalten kann, ist super nützlich, weil… wir langfristige Abhängigkeiten im Markt finden wollen.

In der magischen schwarzen Box

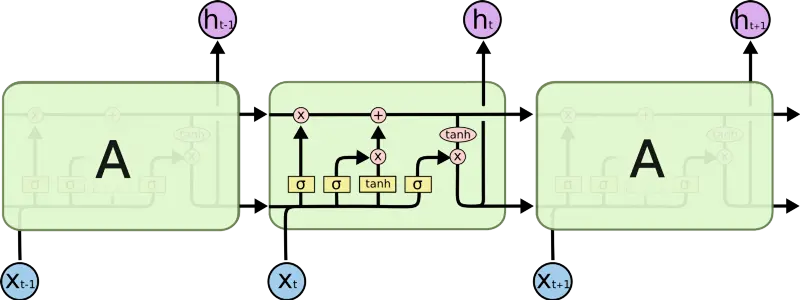
Was ist in dieser magischen schwarzen Box? Es ist eine Art Recurrent Neural Network (RNN) namens LSTM. Ein RNN ist ein Deep-Learning-Algorithmus, der auf Sequenzen arbeitet (wie Sequenzen von Zeichen). Bei jedem Schritt nimmt es eine Repräsentation des nächsten Zeichens (wie die Embeddings, über die wir zuvor gesprochen haben) und verarbeitet diese Repräsentation mit einer Matrix, wie wir es schon gesehen haben. Der Punkt ist: Das RNN hat eine Form von internem Gedächtnis, also merkt es sich, was es zuvor gesehen hat. Es nutzt dieses Gedächtnis, um zu entscheiden, wie genau es auf den nächsten Input operieren soll. Mit diesem Gedächtnis kann das RNN „sich merken“, dass es sich in einem eingerückten Scope befindet – und so erhalten wir korrekt verschachtelten Ausgabetext.

Eine fancy Version eines RNN nennt man Long Short Term Memory (LSTM). LSTM hat clever konstruiertes Gedächtnis, das es ihm erlaubt:

1. Selektiv zu wählen, was es sich merkt
2. Zu entscheiden, zu vergessen
3. Auszuwählen, wie viel seines Gedächtnisses es ausgeben soll.

Ein LSTM kann also ein „{“ sehen und sich sagen: „Oh ja, das ist wichtig, das sollte ich mir merken“, und wenn es das tut, merkt es sich im Wesentlichen einen Hinweis darauf, dass es sich in einem verschachtelten Scope befindet. Sobald es die entsprechende „}“ sieht, kann es entscheiden, die ursprüngliche öffnende Klammer zu vergessen – und damit vergessen, dass es in einem verschachtelten Scope ist.

Wir können dem LSTM beibringen, abstraktere Konzepte zu lernen, indem wir mehrere davon übereinander stapeln – damit wären wir wieder „Deep“. Nun wird jede Ausgabe des vorherigen LSTM zum Input des nächsten LSTM, und jedes lernt höhere Abstraktionen der eingehenden Daten. Im Beispiel oben (und das ist nur illustrative Spekulation) könnte die erste LSTM-Schicht lernen, dass Zeichen, die durch ein Leerzeichen getrennt sind, „Wörter“ sind. Die nächste Schicht könnte Worttypen lernen wie (**static** **void** **action_new_function).**Die nächste Schicht könnte das Konzept einer Funktion und ihrer Argumente lernen und so weiter. Es ist schwer zu sagen, was jede Schicht genau macht, aber Karpathys Blog hat ein wirklich schönes Beispiel dafür, wie er genau das visualisiert hat.

Market2Vec und LSTMs verbinden

Der fleißige Leser wird bemerken, dass Karpathy Zeichen als Inputs verwendet hat, nicht Embeddings (technisch gesehen ein One-Hot-Encoding von Zeichen). Aber Lars Eidnes hat tatsächlich Word Embeddings verwendet, als er Auto-Generating Clickbait With Recurrent Neural Network schrieb.

Die Abbildung oben zeigt das Netzwerk, das er benutzt hat. Ignoriere den SoftMax-Teil (dazu kommen wir später). Für den Moment schau dir an, wie er unten eine Sequenz von Wortvektoren einspeist und jeden einzelnen. (Zur Erinnerung: Ein „Wortvektor“ ist eine Repräsentation eines Wortes in Form einer Reihe von Zahlen, wie wir es am Anfang dieses Posts gesehen haben.) Lars gibt eine Sequenz von Wortvektoren ein, und jeder von ihnen:

1. Beeinflusst das erste LSTM
2. Lässt sein LSTM etwas an das LSTM darüber ausgeben
3. Lässt sein LSTM etwas an das LSTM für das nächste Wort ausgeben

Wir werden dasselbe machen, mit einem Unterschied: Statt Wortvektoren geben wir „MarketVectors“ ein – diese MarketVectors, die wir zuvor beschrieben haben. Zur Wiederholung: Die MarketVectors sollten eine Zusammenfassung dessen enthalten, was zu einem bestimmten Zeitpunkt am Markt passiert. Indem ich eine Sequenz davon durch LSTMs schicke, hoffe ich, die langfristige Dynamik zu erfassen, die im Markt stattgefunden hat. Indem ich mehrere LSTM-Schichten stapel, hoffe ich, höherstufige Abstraktionen des Marktverhaltens zu erfassen.

Was kommt heraus

An dieser Stelle haben wir noch überhaupt nicht darüber gesprochen, wie der Algorithmus eigentlich irgendetwas lernt; wir haben nur über all die cleveren Transformationen gesprochen, die wir mit den Daten machen. Diese Diskussion verschieben wir ein paar Absätze nach unten, aber behalte diesen Teil bitte im Kopf, denn er ist das Setup für die Pointe, die alles andere lohnenswert macht.

In Karpathys Beispiel ist die Ausgabe der LSTMs ein Vektor, der das nächste Zeichen in einer abstrakten Repräsentation darstellt. In Eidnes’ Beispiel ist die Ausgabe der LSTMs ein Vektor, der darstellt, was das nächste Wort in einem abstrakten Raum sein wird. Der nächste Schritt ist in beiden Fällen, diese abstrakte Repräsentation in einen Wahrscheinlichkeitsvektor zu verwandeln – also eine Liste, die sagt, wie wahrscheinlich es ist, dass jeweils das nächste Zeichen bzw. Wort erscheint. Das ist die Aufgabe der SoftMax-Funktion. Sobald wir eine Liste von Wahrscheinlichkeiten haben, wählen wir das Zeichen oder Wort, das am wahrscheinlichsten als Nächstes erscheint.

In unserem Fall, beim „Vorhersagen des Marktes“, müssen wir uns fragen, was genau der Markt vorhersagen soll. Einige Optionen, über die ich nachgedacht habe, waren:

1. Den nächsten Preis für jede der 1000 Aktien vorhersagen
2. Den Wert eines Index (S&P, VIX etc.) in den nächsten n Minuten vorhersagen.
3. Vorhersagen, welche Aktien in den nächsten n Minuten um mehr als x% steigen werden
4. (Mein persönlicher Favorit) Vorhersagen, welche Aktien in den nächsten n Minuten um 2x% steigen/fallen werden, ohne in dieser Zeit um mehr als x% zu fallen/steigen.
5. (Dem wir im Rest dieses Artikels folgen). Vorhersagen, wann der VIX in den nächsten n Minuten um 2x% steigt/fällt, ohne in dieser Zeit um mehr als x% zu fallen/steigen.

1 und 2 sind Regressionsprobleme, bei denen wir eine tatsächliche Zahl vorhersagen müssen statt der Wahrscheinlichkeit eines bestimmten Ereignisses (wie dass der Buchstabe n erscheint oder der Markt steigt). Die sind okay, aber nicht das, was ich machen will.

3 und 4 sind ziemlich ähnlich: Beide fragen nach der Vorhersage eines Ereignisses (im Fachjargon — eines Klassenlabels). Ein Ereignis könnte sein, dass als Nächstes der Buchstabe n erscheint, oder: Ist um 5% gestiegen, ohne in den letzten 10 Minuten mehr als 3% zu fallen. Der Trade-off zwischen 3 und 4 ist, dass 3 viel häufiger ist und daher leichter zu lernen, während 4 wertvoller ist, weil es nicht nur ein Indikator für Profit ist, sondern auch eine Risikobedingung enthält.

5 ist das, womit wir für diesen Artikel weitermachen, weil es ähnlich zu 3 und 4 ist, aber Mechaniken hat, denen leichter zu folgen ist. Der VIX wird manchmal Fear Index genannt und repräsentiert, wie volatil die Aktien im S&P500 sind. Er wird abgeleitet, indem man die implizite Volatilität für bestimmte Optionen auf jede Aktie im Index beobachtet.

Randnotiz — Warum den VIX vorhersagen

Was den VIX zu einem interessanten Ziel macht, ist:

1. Es ist nur eine Zahl im Gegensatz zu 1000en Aktien. Das macht es konzeptionell leichter nachzuvollziehen und reduziert Rechenkosten.
2. Er ist die Zusammenfassung vieler Aktien, also sind die meisten, wenn nicht alle unserer Inputs relevant
3. Er ist keine lineare Kombination unserer Inputs. Implizite Volatilität wird aktienweise aus einer komplizierten, nichtlinearen Formel extrahiert. Der VIX wird aus einer komplexen Formel darauf aufbauend abgeleitet. Wenn wir das vorhersagen können, ist das ziemlich cool.
4. Er ist handelbar, also können wir ihn nutzen, falls das tatsächlich funktioniert.

Zurück zu unseren LSTM-Ausgaben und SoftMax

Wie nutzen wir die Formulierungen, die wir zuvor gesehen haben, um Änderungen im VIX ein paar Minuten in der Zukunft vorherzusagen? Für jeden Punkt in unserem Datensatz schauen wir, was 5 Minuten später mit dem VIX passiert ist. Wenn er um mehr als 1% gestiegen ist, ohne in dieser Zeit um mehr als 0,5% zu fallen, geben wir eine 1 aus, sonst eine 0. Dann erhalten wir eine Sequenz, die so aussieht:

0,0,0,0,0,1,1,0,0,0,1,1,0,0,0,0,1,1,1,0,0,0,0,0 ….

Wir wollen den Vektor, den unsere LSTMs ausgeben, so „quetschen“, dass er uns die Wahrscheinlichkeit liefert, dass der nächste Eintrag in unserer Sequenz eine 1 ist. Dieses Quetschen passiert im SoftMax-Teil des Diagramms oben. (Technisch gesehen, da wir jetzt nur 1 Klasse haben, verwenden wir eine Sigmoid-Funktion).

Bevor wir also dazu kommen, wie das Ding lernt, fassen wir zusammen, was wir bisher gemacht haben:

1. Wir nehmen als Input eine Sequenz von Preisdaten für 1000 Aktien
2. Jeder Zeitpunkt in der Sequenz ist ein Snapshot des Marktes. Unser Input ist eine Liste von 4000 Zahlen. Wir verwenden eine Embedding-Schicht, um die Schlüsselinformationen in nur 300 Zahlen zu repräsentieren.
3. Jetzt haben wir eine Sequenz von Embeddings des Marktes. Wir geben diese in einen Stack von LSTMs, Timestep für Timestep. Die LSTMs erinnern sich an Dinge aus den vorherigen Schritten, und das beeinflusst, wie sie den aktuellen verarbeiten.
4. Wir geben die Ausgabe der ersten LSTM-Schicht in eine weitere Schicht. Diese erinnern sich ebenfalls, und sie lernen höherstufige Abstraktionen der Informationen, die wir hineinstecken.
5. Schließlich nehmen wir die Ausgaben aus allen LSTMs und „quetschen sie“, sodass unsere Sequenz von Marktinformationen zu einer Sequenz von Wahrscheinlichkeiten wird. Die Wahrscheinlichkeit ist: „Wie wahrscheinlich ist es, dass der VIX in den nächsten 5 Minuten um 1% steigt, ohne um 0,5% zu fallen?“

Wie lernt dieses Ding?

Jetzt kommt der spaßige Teil. Alles, was wir bis jetzt gemacht haben, nennt man den Forward Pass: Wir würden all diese Schritte machen, während wir den Algorithmus trainieren, und auch wenn wir ihn in Produktion verwenden. Hier sprechen wir über den Backward Pass – den Teil, den wir nur während des Trainings machen und der unseren Algorithmus lernen lässt.

Während des Trainings haben wir nicht nur jahrelange historische Daten vorbereitet, sondern auch eine Sequenz von Vorhersagezielen – diese Liste aus 0 und 1, die zeigte, ob sich der VIX nach jeder Beobachtung in unseren Daten so bewegt hat, wie wir es wollen.

Um zu lernen, füttern wir die Marktdaten in unser Netzwerk und vergleichen seine Ausgabe mit dem, was wir berechnet haben. In unserem Fall wird der Vergleich einfache Subtraktion sein; das heißt, wir sagen, dass der Fehler unseres Modells ist:

ERROR = (((precomputed)— (predicted probability))² )^(1/2)

Oder auf Deutsch: die Quadratwurzel aus dem Quadrat der Differenz zwischen dem, was tatsächlich passiert ist, und dem, was wir vorhergesagt haben.

Hier ist das Schöne: Das ist eine differenzierbare Funktion; das heißt, wir können sagen, um wie viel sich der Fehler geändert hätte, wenn sich unsere Vorhersage ein wenig geändert hätte. Unsere Vorhersage ist das Ergebnis einer differenzierbaren Funktion – dem SoftMax. Die Inputs in den Softmax, die LSTMs, sind alles mathematische Funktionen, die differenzierbar sind. Nun sind all diese Funktionen voller Parameter – diese großen Excel-Tabellen, von denen ich vor Ewigkeiten gesprochen habe. In diesem Stadium nehmen wir also die Ableitung des Fehlers nach jedem einzelnen der Millionen Parameter in all diesen Excel-Tabellen in unserem Modell. Wenn wir das tun, können wir sehen, wie sich der Fehler ändert, wenn wir jeden Parameter ändern, also ändern wir jeden Parameter so, dass der Fehler sinkt.

Dieses Verfahren propagiert sich bis ganz zum Anfang des Modells. Es optimiert die Art, wie wir die Inputs in MarketVectors einbetten, sodass unsere MarketVectors die bedeutendsten Informationen für unsere Aufgabe repräsentieren.

Es optimiert, wann und was jedes LSTM sich merkt, sodass ihre Ausgaben für unsere Aufgabe am relevantesten sind.

Es optimiert die Abstraktionen, die unsere LSTMs lernen, sodass sie die wichtigsten Abstraktionen für unsere Aufgabe lernen.

Was ich erstaunlich finde, weil wir all diese Komplexität und Abstraktion haben, die wir nirgends explizit spezifizieren mussten. Das wird alles MathaMagically aus der Spezifikation dessen abgeleitet, was wir als Fehler betrachten.

Was kommt als Nächstes

Jetzt, da ich das schriftlich ausgearbeitet habe und es für mich immer noch Sinn ergibt, möchte ich:

1. Sehen, ob sich überhaupt jemand die Mühe macht, das zu lesen.
2. Alle Fehler korrigieren, auf die meine lieben Leser hinweisen
3. Überlegen, ob das noch machbar ist
4. Und es bauen

Also: Wenn du bis hierher gekommen bist, bitte weise auf meine Fehler hin und teile deine Inputs.

Andere Gedanken

Hier sind einige überwiegend fortgeschrittenere Gedanken zu diesem Projekt – welche anderen Dinge ich ausprobieren könnte und warum es mir sinnvoll erscheint, dass das tatsächlich funktionieren könnte.

Liquidität und effiziente Nutzung von Kapital

Im Allgemeinen gilt: Je liquider ein bestimmter Markt ist, desto effizienter ist er. Ich denke, das liegt an einem Henne-und-Ei-Zyklus: Wenn ein Markt liquider wird, kann er mehr Kapital aufnehmen, das hinein- und herausfließt, ohne dass dieses Kapital sich selbst schadet. Wenn ein Markt liquider wird und mehr Kapital darin eingesetzt werden kann, wirst du mehr anspruchsvolle (sophisticated) Akteure sehen, die einsteigen. Das liegt daran, dass es teuer ist, anspruchsvoll zu sein, also musst du Renditen auf einem großen Kapitalblock erzielen, um deine operativen Kosten zu rechtfertigen.

Eine schnelle Folgerung ist, dass in weniger liquiden Märkten die Konkurrenz nicht ganz so anspruchsvoll ist, und daher könnten die Chancen, die ein System wie dieses bringt, noch nicht weg-arbitragiert worden sein. Der Punkt ist: Wenn ich versuchen würde, damit zu handeln, würde ich versuchen, es in weniger liquiden Segmenten des Marktes zu handeln – also vielleicht den TASE 100 statt den S&P 500.

Das Zeug ist neu

Das Wissen über diese Algorithmen, die Frameworks zu ihrer Ausführung und die Rechenleistung, um sie zu trainieren, sind alle neu – zumindest insofern, als sie dem durchschnittlichen Joe wie mir zur Verfügung stehen. Ich würde annehmen, dass die Top-Player das vor Jahren herausgefunden haben und auch schon lange die Kapazität hatten, es auszuführen; aber wie ich im Absatz oben erwähnt habe, agieren sie wahrscheinlich in liquiden Märkten, die ihre Größe tragen können. Die nächste Stufe von Marktteilnehmern, nehme ich an, hat eine geringere Geschwindigkeit der technologischen Assimilation, und in diesem Sinne gibt es – oder wird es bald geben – ein Rennen, das in bisher unerschlossenen Märkten umzusetzen.

Mehrere Zeitrahmen

Obwohl ich oben einen einzelnen Input-Stream erwähnt habe, stelle ich mir vor, dass ein effizienterer Trainingsweg wäre, Marktvektoren (mindestens) auf mehreren Zeitrahmen zu trainieren und sie in der Inferenzphase einzuspeisen. Das heißt: Mein niedrigster Zeitrahmen wäre alle 30 Sekunden gesampelt, und ich würde erwarten, dass das Netzwerk Abhängigkeiten lernt, die sich höchstens über Stunden erstrecken.

Ich weiß nicht, ob sie relevant sind oder nicht, aber ich denke, es gibt Muster auf mehreren Zeitrahmen, und wenn die Rechenkosten niedrig genug gebracht werden können, lohnt es sich, sie ins Modell zu integrieren. Ich ringe noch damit, wie man diese am besten im Computational Graph repräsentiert, und vielleicht ist es nicht zwingend nötig, damit anzufangen.

MarketVectors

Wenn wir Wortvektoren in NLP verwenden, starten wir normalerweise mit einem vortrainierten Modell und passen die Embeddings während des Trainings unseres Modells weiter an. In meinem Fall gibt es keine vortrainierten Marktvektoren, noch gibt es einen klaren Algorithmus, um sie zu trainieren.

Meine ursprüngliche Überlegung war, einen Auto-Encoder zu verwenden, wie in diesem Paper, aber End-to-End-Training ist cooler.

Eine ernsthaftere Überlegung ist der Erfolg von Sequence-to-Sequence-Modellen in Übersetzung und Spracherkennung, bei denen eine Sequenz schließlich als einzelner Vektor kodiert und dann in eine andere Repräsentation dekodiert wird (wie von Sprache zu Text oder von Englisch zu Französisch). In dieser Sicht ist die gesamte Architektur, die ich beschrieben habe, im Wesentlichen der Encoder, und ich habe keinen Decoder wirklich ausgearbeitet.

Aber ich will mit der ersten Schicht etwas Spezifisches erreichen – der Schicht, die den 4000-dimensionalen Vektor als Input nimmt und einen 300-dimensionalen ausgibt. Ich will, dass sie Korrelationen oder Beziehungen zwischen verschiedenen Aktien findet und Features darüber zusammensetzt.

Die Alternative wäre, jeden Input durch ein LSTM zu schicken, vielleicht alle Output-Vektoren zu konkatenieren und das als Output der Encoder-Phase zu betrachten. Ich denke, das wäre ineffizient, weil die Interaktionen und Korrelationen zwischen Instrumenten und ihren Features verloren gehen würden, und es würde 10x mehr Rechenaufwand erfordern. Andererseits könnte so eine Architektur naiv über mehrere GPUs und Hosts parallelisiert werden, was ein Vorteil ist.

CNNs

In letzter Zeit gab es einen Schub an Papers zu zeichenbasierter maschineller Übersetzung. Dieses Paper ist mir ins Auge gefallen, weil sie Langstreckenabhängigkeiten mit einer Convolutional-Schicht statt einem RNN erfassen. Ich habe es nur kurz gelesen, aber ich denke, eine Modifikation, bei der ich jede Aktie als Kanal behandle und zuerst über Kanäle falte (wie bei RGB-Bildern), wäre eine weitere Möglichkeit, die Marktdynamik zu erfassen – auf ähnliche Weise, wie sie im Wesentlichen semantische Bedeutung aus Zeichen kodieren.